前回の続きです。
F9連打ではアニメーションとしては味気ないので、マクロ機能を活用して、自動的にグラフが更新されるようにしていきます。
準備段階:エクセルマクロを使用可能にする
とりあえず、エクセルのマクロを使用可能にします。説明は以下参考記事を参照してください。
- https://support.microsoft.com/ja-jp/office/microsoft-365-%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB%E3%81%A7%E3%83%9E%E3%82%AF%E3%83%AD%E3%82%92%E6%9C%89%E5%8A%B9%E3%81%BE%E3%81%9F%E3%81%AF%E7%84%A1%E5%8A%B9%E3%81%AB%E3%81%99%E3%82%8B-12b036fd-d140-4e74-b45e-16fed1a7e5c6
- https://www.pref.saitama.lg.jp/documents/119761/macyuukouka.pdf
マクロ使用の目的
ここまでの復習です。以下の\(P_2(t)\)をエクセルの散布図として\(X\)\(Y\)平面上にグラフ化し、定数としていた\(R_1\)、\(\omega_1\)、\(R_2\)、\(\omega_2\)を連続して適当に変化させることで、グラフ描画を連続的に変化させることが目的でした。
\(P_2(t)= (R_1 cos(\omega_1 t) + R_2 cos(\omega_2 t),R_1 sin(\omega_1 t)+R_2 sin(\omega_2 t))\)
\(R_1\)、\(\omega_1\)、\(R_2\)、\(\omega_2\)の変化のさせ方は、単純な乱数でも全く問題ありません。やはりそれでは面白くないので、ある程度連続的に変化するように工夫します。
連続して適当に変化する乱数の生成
試しに、0~1の範囲での乱数を180回連続して並べてみます。横軸が何度目の乱数か、縦軸が乱数の値とすると、下図のようになりました。
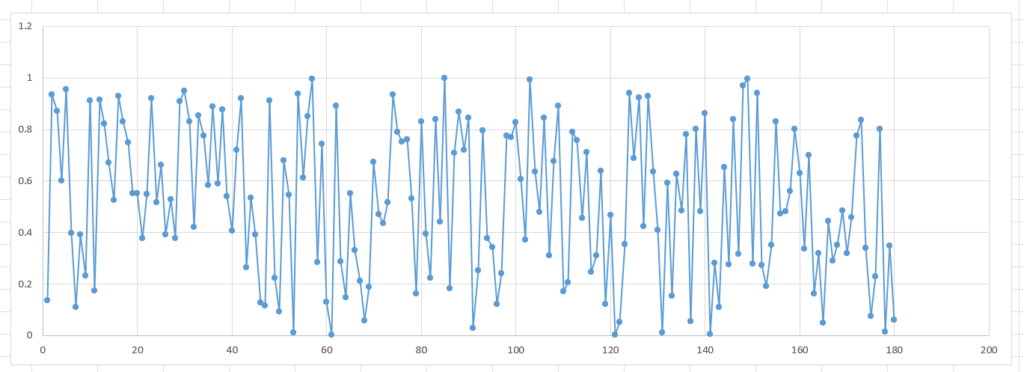
エクセルの散布図をある程度連続的に変化するようにとすると、単純なランダムな数字の列は望ましくなく、下図のイメージにあるようにある程度、数値変化に連続性があることが望ましいと言えます。
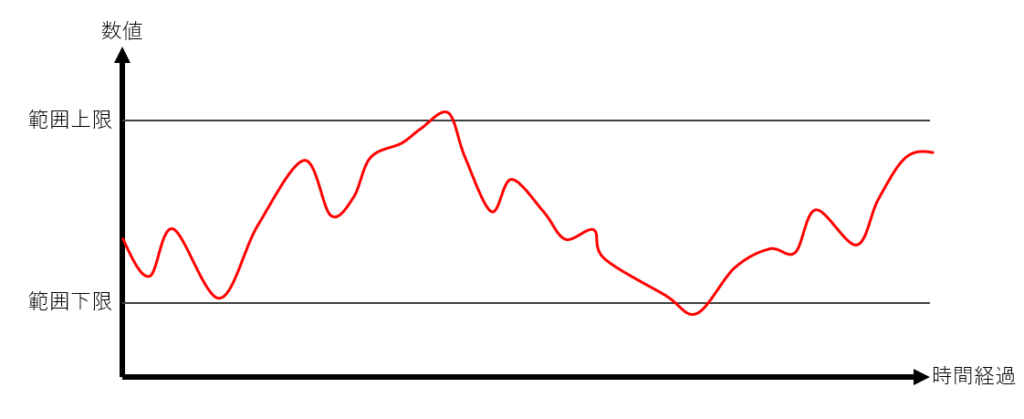
そこで、ある位置変数\(x\)と考え、\(x\)が時刻\(\tau\)に従って、変化することとします。さらに、\(x(\tau)\)の速度、加速度を考え、変数を\(v(\tau)=\displaystyle \frac{dx}{d\tau}(\tau), a(\tau)=\displaystyle \frac{dv}{d\tau}(\tau)\)とします。ここで、時刻\(\tau\)は、\(P_2(t)\)の時刻\(t\)と区別するために別の変数としています。
\(x(\tau), v(\tau), a(\tau)\)は離散化して、乱数的に生成した\(a(\tau)\)を逐次足し合わせて積分するとします。\(i\)を自然数として
離散時間:\(\tau_{i+1} = \tau_i + \Delta \tau\)
[0]初期値:\(x(\tau_1) = 0, v(\tau_1) = 0, a(\tau_1) = 0\)
[1]加速度:\(a(\tau_{i+1}) = a(\tau_i) + Rnd(\tau_i)\)
[2]速度:\(v(\tau_{i+1}) = v(\tau_i) + \Delta a(\tau_{i+1})\)
[3]位置:\(x(\tau_{i+1}) = x(\tau_i) + \Delta v(\tau_{i+1})\)
とします。\(Rnd(\tau_i)\)は、時刻\(\tau_i\)において、\(-1\)以上、\(+1\)未満の数値をランダムに返すものとします。これで[0][1][2][3][1][2][3][1][2][3] …を繰り返し計算すれば、適当に連続した乱数列\(X_i\)が得られます。なお、初期値は適当でよいのですが、最初から大きな値を設定すると発散しがちですのでとりあえず\(0\)としておくのが無難です。
このような\(X_i\)をいくつか作って、\(R_1\)、\(\omega_1\)、\(R_2\)、\(\omega_2\)に設定すると、エクセルの散布図がある程度連続的に変化して見えるようになります。
上の[0][1][2][3][1][2][3][1][2][3] …を実際にやってみました。
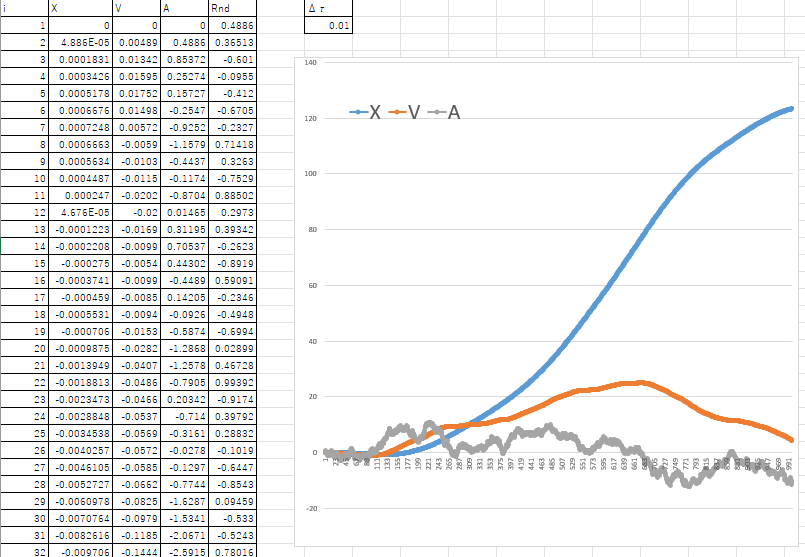
\(\tau_{i+1}\)はそれなりに、滑らかに変化しているので良いことにします。